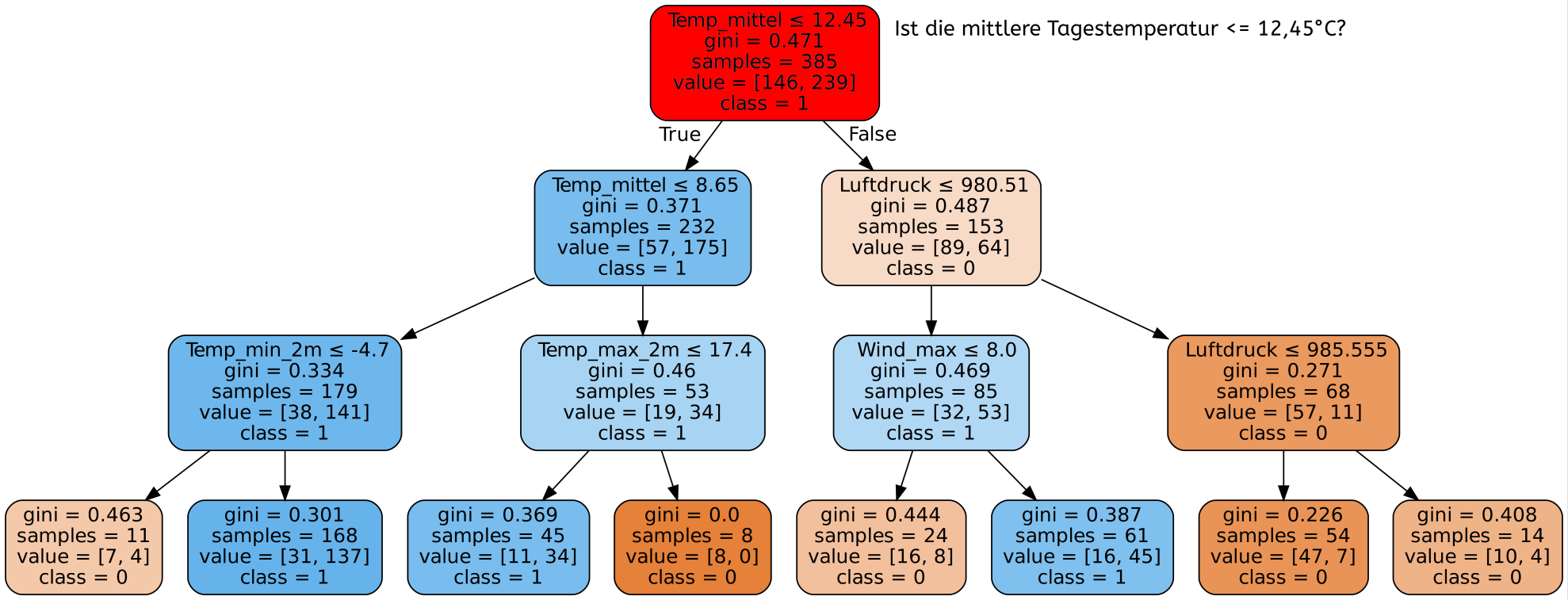
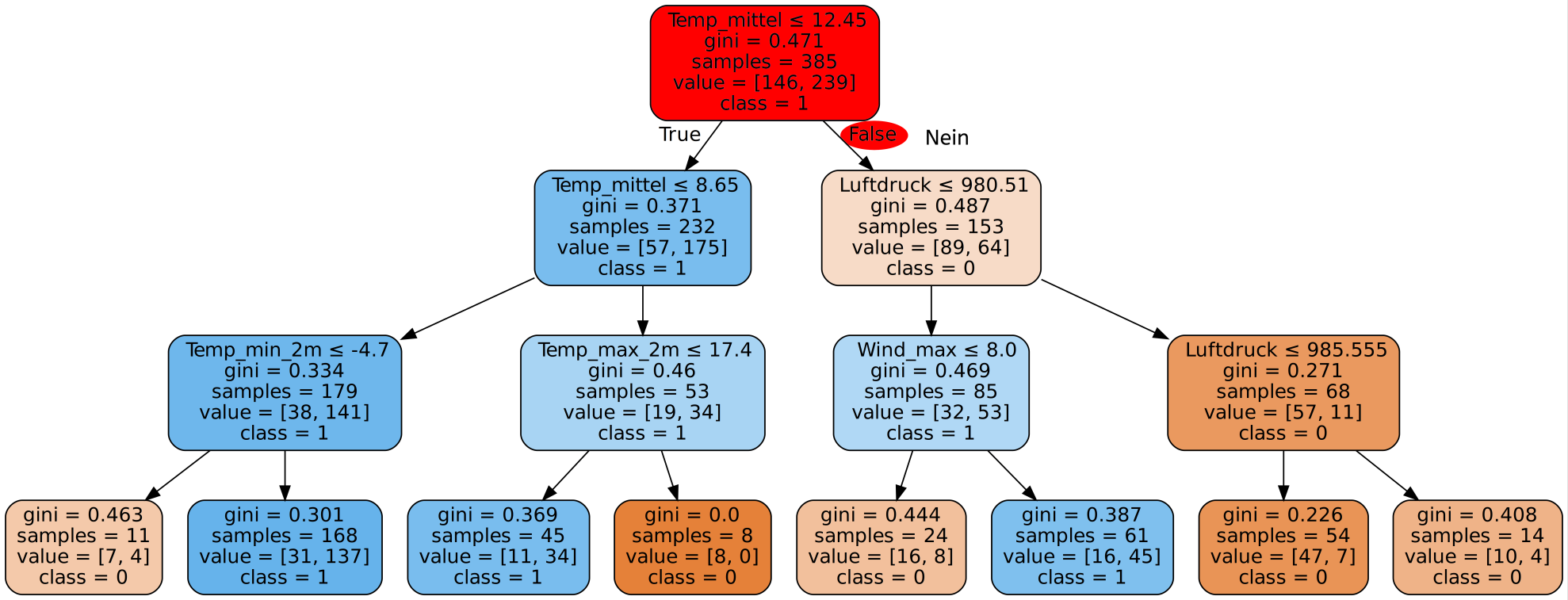
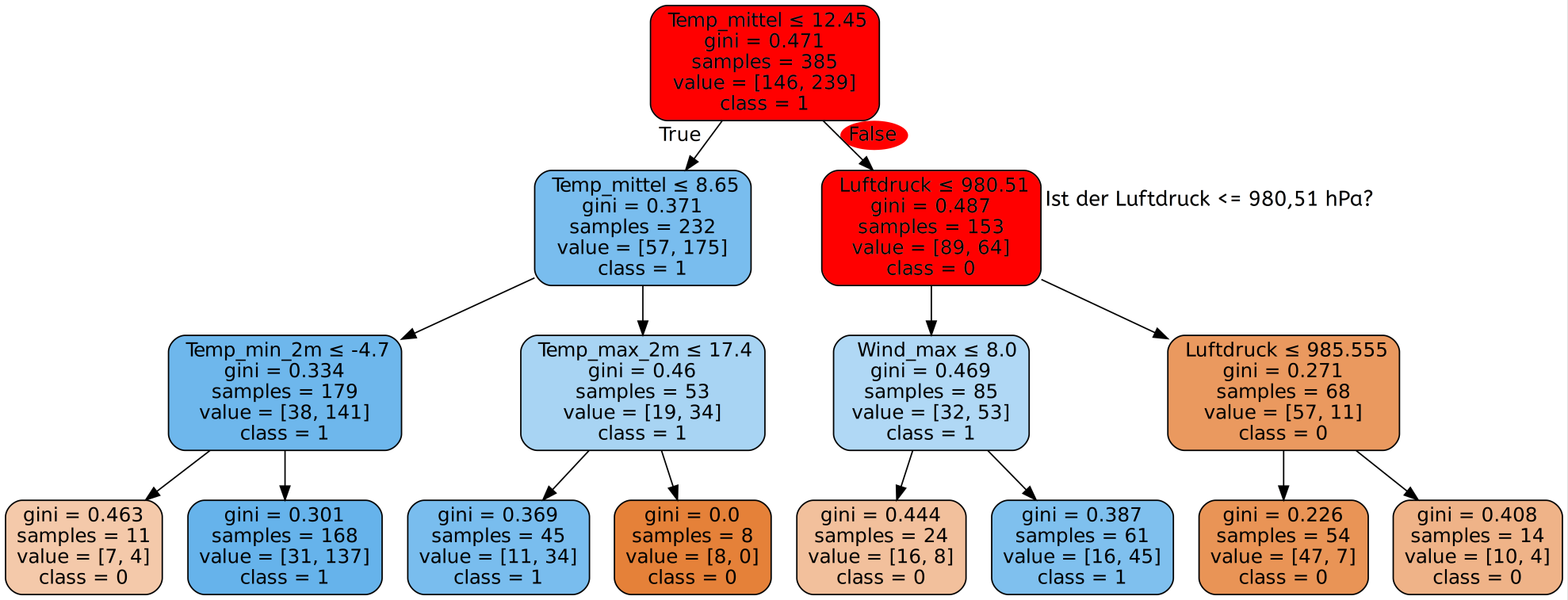
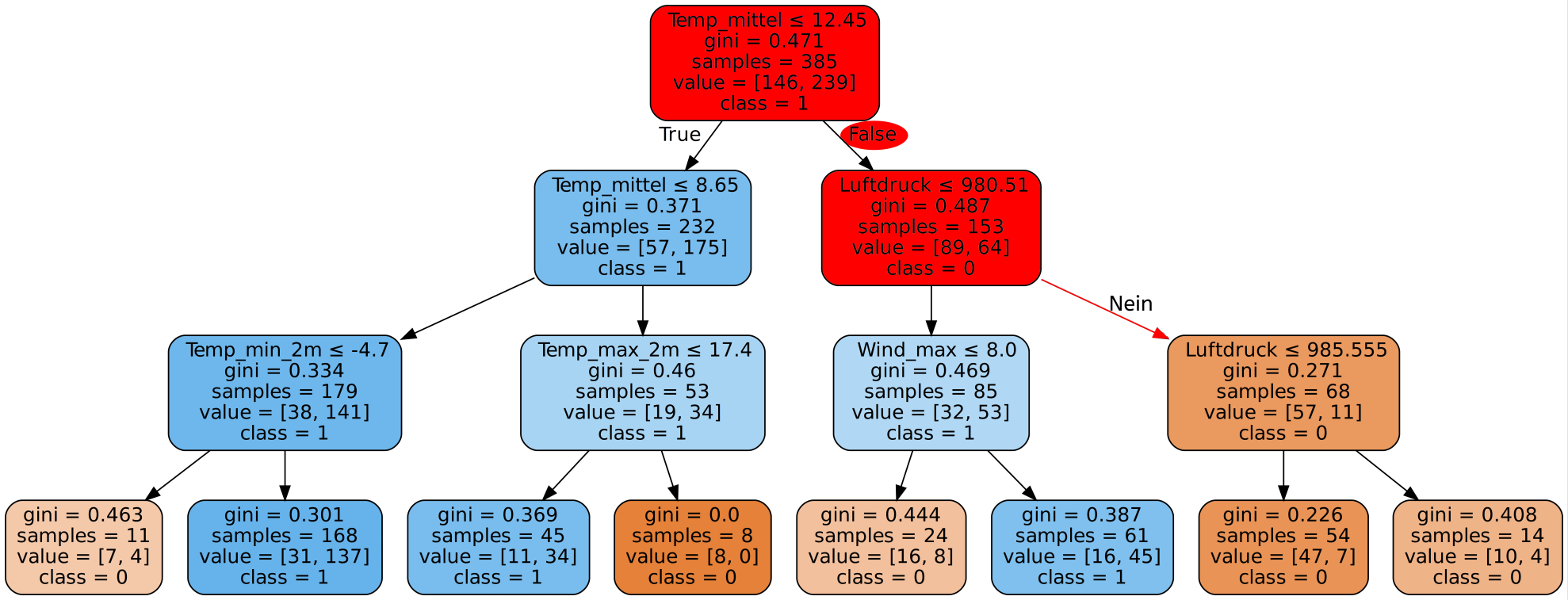
Sensitivität und Spezifität
Auf den Testdaten erreichen wir eine Genauigkeit von ca. 75%. Dabei gibt es sowohl Tage ohne Niederschlag für die unser Programm fälschlicherweise Niederschlag vorhersagt (falsch positive Ergebnisse), als auch umgekehrt (falsch negative Ergebnisse).

In diesem Zusammenhang sind zwei Begriffe von Bedeutung: Sensitivität und Spezifität. Diese geben neben der generellen Genauigkeit eine weitere Möglichkeit die Qualität der Vorhersagen zu überprüfen.
Die Sensitivität ist die Wahrscheinlichkeit, mit der unser Programm einen Tag an dem es Niederschlag gibt korrekt vorhersagt.
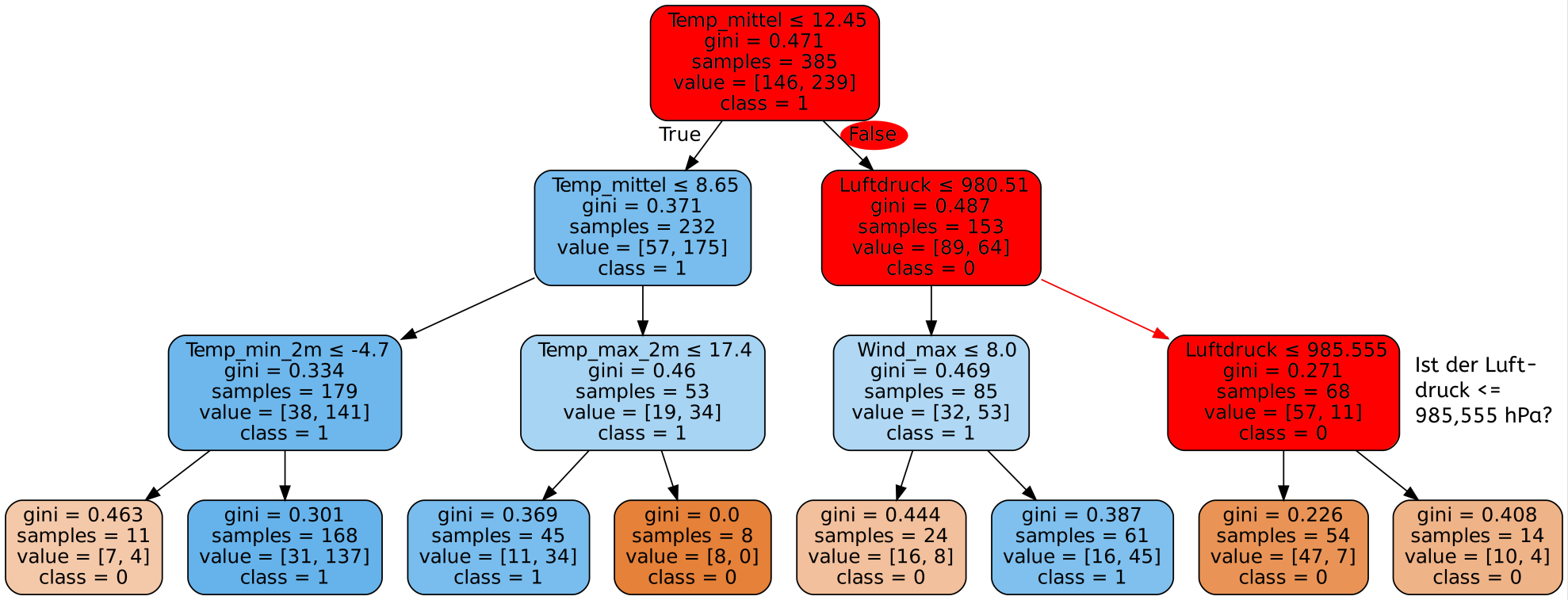
Im Bild oben gilt also: Sens = 3526 / (3526 + 808) ≈ 0,8136 = 81,36%
Die Spezifität ist die Wahrscheinlichkeit, mit der unser Programm einen Tag ohne Niederschlag korrekt vorhersagt.
Spez = 1701 / (1701 + 883) ≈ 0,6583 = 65,83%
Wie wir sehen ist unser Programm also besser beim Erkennen von Tagen mit Niederschlag als von Tagen ohne Niederschlag.
Wenn wir uns bei der Entscheidung, ob wir morgens einen Regenschirm mitnehmen, auf unser Programm verlassen würden, hätte dies zur Folge, dass wir also an 100% - 81,36% = 18,64% der Tage an denen es regnet nass werden. Andererseits würden wir an 34,17% aller sonnigen Tage unnötigerweise einen Schirm mitnehmen.
Insgesamt ist das auf Dauer kein zufriedenstellender Zustand und wir würden vermutlich wieder dazu übergehen uns auf unser Gefühl zu verlassen oder die offizielle Wettervorhersage des Deutschen Wetterdienstes zu Rate ziehen. Damit wäre unsere gesamte Arbeit beim Programmieren umsonst gewesen.
Zum Glück gibt es Hilfsmittel die es uns erlauben den Entscheidungsbaum zu beeinflussen. Diese Hilfsmittel sind die sogenannten Parameter. Einer dieser Parameter ist der Schwellenwert.
Dieser Wert gibt dem Algorithmus die Anweisung, wann er einen Tag als Tag mit oder ohne Niederschlag angeben soll. Zunächst wird der Algorithmus ganz normal durchlaufen und der Entscheidungsbaum aufgebaut. Allerdings wird gleichzeitig für jeden Tag die Wahrscheinlichkeit berechnet mit der er ein Tag mit Niederschlag ist. Der Schwellenwert gibt dann vor, ab welcher Wahrscheinlichkeit ein Tag schlussendlich als Tag mit Niederschlag im Entscheidungsbaum klassifiziert werden soll.
Beispiel:
Für einen bestimmten Tag hat unser Algorithmus berechnet, dass die Wahrscheinlichkeit dass er als Tag mit Niederschlag eingeordnet wird 0,60 = 60% beträgt. Er hält Regen an diesem Tag also für wahrscheinlicher als Sonne. Damit wird dieser Tag standardmäßig im Entscheidungsbaum als Tag mit Niederschlag auftauchen. Wie vermutlich die meisten von uns dies intuitiv tun würden, ist der voreingestellte Schwellenwert 50%. Jeder Tag mit einer berechneten Wahrscheinlichkeit von mehr als 50% dass es regnet, wird also auch als Tag mit Niederschlag klassifiziert. Wenn wir diesen Schwellenwert nun von Hand anpassen, können wir dafür sorgen, dass beispielsweise bereits alle Tage mit einer Wahrscheinlichkeit von nur 20% als Tag mit Niederschlag eingeordnet werden oder eben erst mit 70%.
Dies hat natürlich massive Auswirkungen auf die Vorhersagen unseres Entscheidungsbaums.
Je geringer der Schwellenwert gesetzt wird, desto mehr Tage werden als Tag mit Niederschlag vorhergesagt. Damit steigt die Sensitivität des Programms, da die Anzahl der falsch als Tag ohne Niederschlag vorhergesagten Tage sinkt. Diese Tage (im Bild oben die 808 Tage) werden als falsch negative Ergebnisse des Programms bezeichnet. Je höher der Schwellenwert, desto höher muss die Wahrscheinlichkeit für Niederschlag sein, damit der Tag auch tatsächlich als Tag mit Niederschlag klassifiziert wird. Das bedeutet einen Anstieg der Spezifität, da die Zahl der falsch positiven Ergebnisse reduziert wird (im Bild die 883 Tage).
Ideal wäre es natürlich, wenn sowohl die Spezifität als auch die Sensitivität hoch wären. Wir werden über Anpassungen des Schwellenwerts allerdings nicht sowohl 100% Sensitivität als auch 100% Spezifität gleichzeitig erreichen. Da wir wissen, dass wir die Sensitivität erhöhen können, indem wir den Schwellenwert kleiner machen, könnten wir natürlich solange verschiedene Werte ausprobieren, bis wir einen guten Kompromiss zwischen Sensitivität und Spezifität gefunden haben. Wir können uns aber auch zuerst die folgenden Grafiken anschauen:
Warum können nicht sowohl Sensitivität als auch Spezifität gleichzeitig bei 100% liegen?
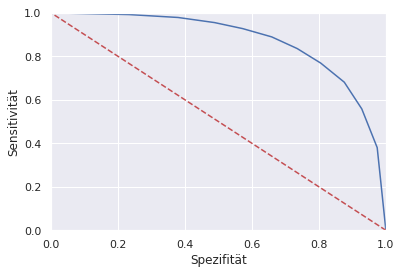
Hier wird der Zusammenhang zwischen Spezifität und Sensitivität sehr deutlich. Je höher die Spezifität, desto niedriger ist die Sensitivität - und umgekehrt. Wenn wir eine Spezifität von 80% haben, erreichen wir nur noch eine Sensitivität von ca. 75%. Das bedeutet, dass 20% aller Tage ohne Niederschlag und 25% aller Tage mit Niederschlag nicht richtig erkannt werden. Aus diesem Graphen ist allerdings noch nicht ersichtlich bei welchen Schwellenwerten die jeweilige Sensitivität und Spezifität erreicht wird. Daher müssen wir uns Sensitivität und Spezifität einzeln anschauen.
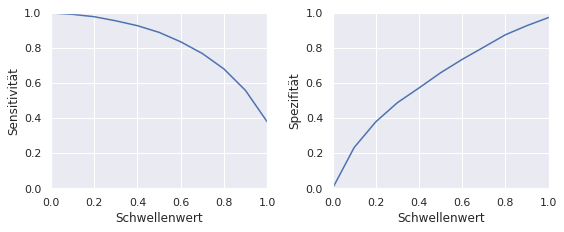
Die 75% Sensitivität und 80% Spezifität erreichen wir mit einem Schwellenwert von ungefähr 0.7.
Mit Hilfe dieser Graphen haben wir eine gute Übersicht über die Entwicklung der möglichen Sensitivitäten und Spezifitäten. Jetzt müssen wir uns nur noch für einen bestimmten Schwellenwert entscheiden der in unserem Szenario optimal ist.
Aber was ist ein optimaler Schwellenwert?
Auf diese Frage gibt es keine allgemeingültige Antwort. Es hängt immer vom Anwendungsfall und der Fragestellung ab, was als optimal zu bezeichnen ist. In unserem Beispiel könnte man sagen, dass es schlimmer ist nass zu werden weil man sich fälschlicherweise auf Sonne vorbereitet hat und keinen Schirm mitgenommen hat, als dass die Sonne scheint obwohl man sich auf Regen eingestellt hat. Das würde bedeuten, dass es sinnvoller ist möglichst die Sensitivität zu verbessern damit wirklich (so gut wie) alle Tage mit Niederschlag auch als solche erkannt werden. Der Schwellenwert sollte somit möglichst klein sein. Das hat dann allerdings zur Folge, dass die Spezifität sinkt und man unnötigerweise an einigen Tagen auf Regen eingestellt ist. Manche werden dies jedoch bevorzugen, da sie sich eher freuen, wenn es unverhofft doch nicht regnet.
Bei anderen überwiegt aber vielleicht der Ärger den ganzen Tag einen nicht genutzten Schirm oder Regenjacke dabei zu haben. Für diese Gruppe wäre eine Optimierung der Spezifität sinnvoller - also ein möglichst hoher Schwellenwert. Sie müssen dann allerdings damit umgehen können, dass sie teilweise keinen Schirm oder Ähnliches dabei haben, obwohl es regnet.
In den beiden Extremfällen, bei denen der Schwellenwert auf 0 bzw. 1 gesetzt wird, werden entweder alle Tage als Tage mit Niederschlag klassifiziert oder alle Tage als Tage ohne Niederschlag.
Ein Kompromiss beider Ansätze ist ebenfalls denkbar, bei dem es um eine möglichst gute Ausgewogenheit geht. Weder soll die Spezifität noch die Sensitivität bevorzugt werden. Dies würden wir bei unserem Programm mit einem Schwellenwert von ungefähr 0.7 erreichen.
Neben dem Schwellenwert gibt es noch andere Parameter bei Decision Trees.